Valeur qui est générée sur le montant d’un capital variable et qui est appliquée sur un investissement ou un crédit.
Quel est l’intérêt composé?
L’intérêt composé est la valeur qui est générée sur le montant d’un capital variable et qui est appliquée sur un investissement ou un crédit .
Elle est dite composée car elle est calculée sur la valeur d’un capital qui augmente constamment, car les intérêts s’additionnent à chaque période. Ce concept est applicable pour calculer combien est gagné dans un investissement ou une épargne , ainsi que pour calculer combien est payé dans un prêt ou un crédit.
Sa principale caractéristique est que l’intérêt calculé varie constamment de façon exponentielle et s’ajoute à la valeur du capital de chaque période (capitalisation). Par conséquent, les intérêts seront toujours plus élevés à chaque période de temps .
Ci-dessous, vous pouvez voir un exemple de ces concepts, qui montre le comportement d’un capital de 800 $ avec un taux d’intérêt composé de 2 % pendant 5 périodes :
| Période | valeur en capital | Taux d’intérêt | Intérêts de période complexe |
|---|---|---|---|
| 1 | 800,00 $ | deux% | 16,00 $ |
| deux | 816,00 $ | deux% | 16,32 $ |
| 3 | 832,32 $ | deux% | 16,65 $ |
| 4 | 848,97 $ | deux% | 16,98 $ |
| 5 | 865,95 $ | deux% | 17,32 $ |
Dans le graphique ci-dessus, nous pouvons voir que la valeur du capital et des intérêts augmentent successivement et varient à chaque période de temps, en raison de la capitalisation des intérêts.
Formule pour calculer les intérêts composés
La formule générale de calcul des intérêts composés est la suivante :
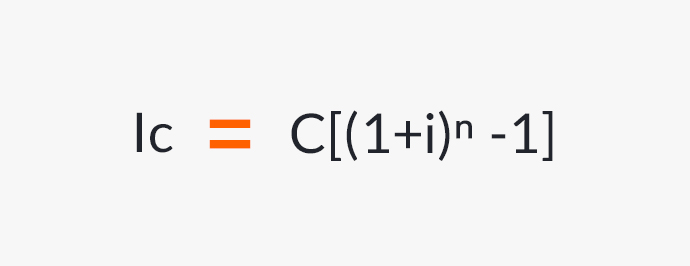
Formule pour calculer les intérêts composés.
Les variables qui impliquent la formule précédente sont :
- Le capital (C) : montant initial de la valeur délivrée sous forme de prêt ou d’investissement.
- Le taux d’intérêt (i) de la période, exprimé sous forme décimale.
- Temps (n) : nombre de périodes de temps.
Pour appliquer la formule ci-dessus, il faut tenir compte du fait que le taux d’intérêt et le nombre de périodes doivent être exprimés dans la même unité de temps .
Dans les cas où le taux d’intérêt et le nombre de périodes ne sont pas exprimés dans la même unité de temps, avant d’appliquer la formule, il faudra calculer le taux d’intérêt applicable à chaque période de capitalisation, comme suit :

Les variables impliquées dans cette formule sont :
- L’intérêt proportionnel (i) : le taux d’intérêt applicable à chaque période de capitalisation.
- L’intérêt (j) : taux d’intérêt annuel.
- Le temps (m) : la fréquence à laquelle les intérêts seront capitalisés par rapport à une année.
Intérêt composé et intérêt simple
- Article détaillé : Intérêt simple .
Les principales différences entre l’intérêt composé et l’intérêt simple sont les suivantes :
- Dans l’intérêt composé, la valeur du capital varie et augmente constamment, car l’intérêt calculé à chaque période s’ajoute. Au lieu de cela, l’intérêt simple est calculé sur la valeur du capital initial, qui reste inchangée.
- Dans les intérêts composés , les intérêts génèrent plus d’intérêts , tandis que dans les intérêts simples, les intérêts ne génèrent pas plus d’intérêts.
- Dans l’intérêt composé, il est ajouté au principal à chaque période de temps , dans l’intérêt simple, il n’est pas ajouté au principal.
- Dans l’intérêt composé , l’intérêt calculé varie , augmentant à chaque période calculée. En intérêt simple, les intérêts calculés à chaque période sont toujours les mêmes, c’est-à-dire qu’ils ne présentent pas de variations.
À titre d’exemple, voyons comment les deux intérêts se comportent avec la même valeur en capital :
| Intérêt simple | |||
| Période | valeur en capital | Taux d’intérêt | Intérêt simple de la période |
| 1 | 800 $ | deux% | 16 $ |
| deux | 800 $ | deux% | 16 $ |
| 3 | 800 $ | deux% | 16 $ |
| 4 | 800 $ | deux% | 16 $ |
| 5 | 800 $ | deux% | 16 $ |
| Intérêts composés | |||
| Période | valeur en capital | Taux d’intérêt | Intérêts de période complexe |
| 1 | 800 $ | deux% | 16,00 $ |
| deux | 816 $ | deux% | 16,32 $ |
| 3 | 832 $ | deux% | 16,65 $ |
| 4 | 848 $ | deux% | 16,98 $ |
| 5 | 865 $ | deux% | 17,32 $ |
Exemples de calcul d’intérêts composés
Exemple 1 : Scandina Enterprises a reçu un nouveau prêt d’investissement gratuit d’une valeur de 7 800 $ et doit payer des intérêts composés à un taux de 25 % par an pendant 3 ans, composés annuellement. Quelle est la valeur que vous devez payer pour les intérêts ?
- Ic = C [ (1 + je) n – 1]
- Ic = 7 800 [ (1 + 0,25) 3 – 1]
- Est = 7 434,38 $
Réponse : le montant à payer pour les intérêts composés sur 3 ans est de 7 434,38 $.
Exemple 2 : L’entreprise Scandina Enterprises a reçu un nouveau crédit d’investissement gratuit d’une valeur de 7 800 $ et doit payer des intérêts composés au taux de 25 % par année pendant 36 mois, dont la fréquence de capitalisation est mensuelle. Quelle est la valeur que vous devez payer pour les intérêts ?
Nous convertissons d’abord le taux d’intérêt applicable à chaque mois :
- je = j/m
- je = 0,25/12
- je = 0,02083
Maintenant que nous avons le temps et le taux exprimés dans la même unité de temps, dans ce cas en mois, nous pouvons appliquer la formule des intérêts composés :
- Ic= C [ (1 + je) n – 1]
- Ic= 7,800 [ (1 + 0,02083) 36 – 1]
- IC = 8 585,84
Réponse : le montant à payer pour les intérêts composés sur les 36 mois est de 8 585,84 $.
| Bibliographie: |
|---|
|