La valeur qui apparaît le plus grand nombre de fois dans un ensemble de données.
Qu’est-ce que le mode statistique ?
Le mode statistique est la valeur qui, dans un ensemble de données, est répétée le plus grand nombre de fois.
La détermination du mode statistique dans un ensemble de données non groupées ne nécessite aucun type de calcul, mais uniquement le comptage des variables. Une autre façon de déterminer le mode dans des données non groupées consiste à rechercher la valeur de fréquence la plus élevée dans un tableau de fréquence absolue .
Le mode statistique est applicable aux données qualitatives et quantitatives.
Types de modes statistiques
Le mode statistique est classé comme suit :
- Mode unimodal : type de mode statistique dans lequel une seule valeur apparaît le plus grand nombre de fois dans un ensemble de données.
- Mode bimodal : type de mode statistique dans lequel 2 valeurs différentes ont le même nombre maximum de répétitions, au sein d’un jeu de données.
- Mode multimodal : type de mode statistique dans lequel 3 valeurs différentes ou plus ont le même nombre maximal de répétitions au sein d’un ensemble de données.
Mode statistique sur données groupées
Lorsque les données d’un ensemble sont regroupées en intervalles, le mode statistique correspond au milieu de l’intervalle qui présente la fréquence la plus élevée.
Compte tenu de ce qui précède, la première étape pour calculer le mode dans les données groupées consiste à déterminer quel est l’intervalle avec la fréquence la plus élevée dans le tableau qui contient les informations groupées.
Par la suite, le calcul du mode est effectué à l’aide de la formule suivante :
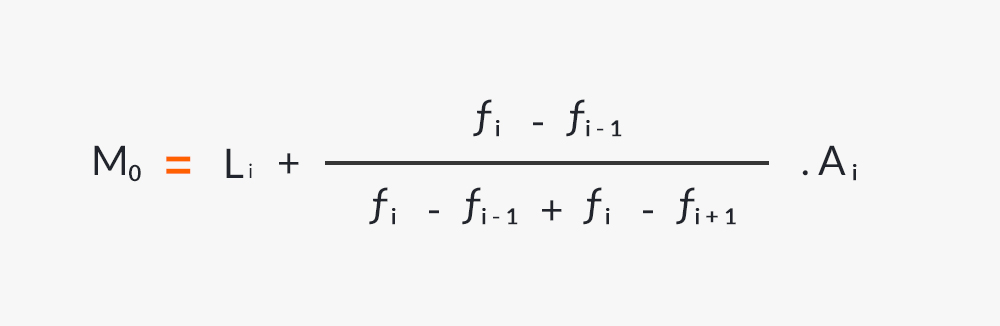
Formule pour calculer le mode statistique.
Les variables qui impliquent l’équation précédente sont :
- Li : limite inférieure de l’intervalle où se situe le mode.
- fi-1 : fréquence absolue de l’intervalle précédent où se situe le mode.
- fi : fréquence absolue de l’intervalle où se situe le mode.
- fi+ 1 : fréquence absolue du prochain intervalle où se situe le mode.
- Ai : amplitude de l’intervalle où se trouve le mode.
Exemples de mode statistique
Quelques exemples de mode statistique sont les suivants, prenant le cas d’un consultant qui décide d’effectuer des recherches dans un bureau.
Exemple de mode unimodal
Nombre d’enfants possédés par les employés. Après avoir posé la question à 20 employés, le jeu de données est le suivant : [ 0, 2, 2, 0, 3, 5, 1, 2, 3, 1, 0, 2, 6, 4, 3, 4, 2, 0 , 1, 2].
Le mode de l’ensemble est 2, puisque cette valeur est répétée 6 fois, tandis que le reste des valeurs est répété un plus petit nombre de fois.
Exemple de mode bimodal
Âge des employés. Après avoir posé la question à 20 salariés, le jeu de données est le suivant : [25, 27, 25, 30, 28, 25, 30, 25, 32, 42, 51, 25, 27,30, 33, 30, 42, 40 , 51, 30].
Ainsi, le mode de l’ensemble est 25 et 30, puisque les deux sont répétés 5 fois tandis que le reste des valeurs est répété un plus petit nombre de fois.
Exemple de mode multimodale
Nombre de pièces de leur logement. Après avoir posé la question à 20 employés, le jeu de données est le suivant : [2, 3, 2, 2, 4, 1, 3, 3, 2, 3, 6, 5, 4.4, 2, 1, 1, 4, 4 , 3].
Le mode de l’ensemble est 2 , 3 et 4, puisque ces valeurs sont répétées 5 fois, tandis que les autres sont répétées un plus petit nombre de fois.
Exemple de mode dans les données groupées
Combien coûte le poids en kilos des employés. Après avoir posé la question à 20 salariés, le jeu de données est le suivant :
| Kilogrammes | Fréquence absolue (Fa) |
| [50 – 60] | 1 |
| [60 – 70] | 4 |
| [70 – 80] | deux |
| [80 – 90] | 8 |
| [90 – 100] | 5 |
| Somme ∑ | vingt |
Pour ce calcul du mode statistique nous appliquons les étapes suivantes :
- L’intervalle où se trouve la fréquence absolue la plus élevée se situe, en l’occurrence dans l’intervalle [80 – 90] de fréquence 8.
- La formule est appliquée pour calculer le mode dans les données groupées :
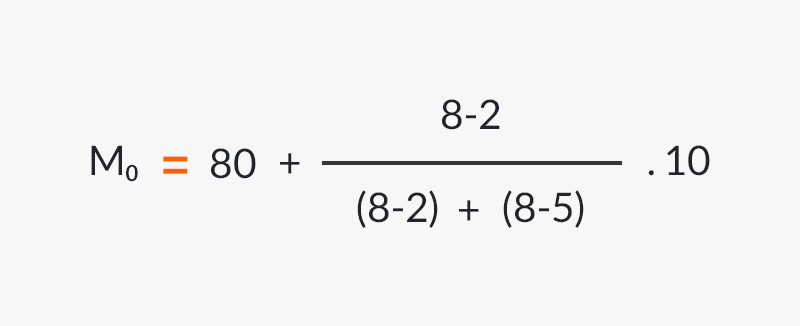
On obtient ainsi que le mode statistique est 87 .
| Bibliographie: |
|---|
|