Moyenne obtenue en additionnant toutes les données et en la divisant par la quantité totale de données.
Quelle est la moyenne arithmétique ?
La moyenne arithmétique, également appelée moyenne , est la valeur obtenue en additionnant toutes les données et en la divisant par la quantité totale de données.
L’un des problèmes fondamentaux auquel est confrontée une analyse statistique consiste à rechercher une valeur représentative d’une série de valeurs ; c’est-à-dire que si vous avez une quantité qui varie, soit dans l’espace, soit dans le temps, vous devrez obtenir son niveau prédominant.
La valeur fournie par cette année scolaire ou ce niveau prédominant est la moyenne .
Lorsque la moyenne arithmétique est calculée, la variation est négligée et seule la valeur prédominante est intéressante , ce qui est un grand avantage dans le résumé statistique.
La valeur de la moyenne arithmétique dépend de chacune des mesures qui composent la série et est affectée par des écarts extrêmes par rapport à la moyenne.
Utilisations de la moyenne arithmétique
Les utilisations de la moyenne arithmétique sont les suivantes :
- La moyenne arithmétique est la moyenne la plus utilisée car elle peut être calculée pour tout type de progression , logiquement de préférence celles qui suivent une progression arithmétique.
- Il est applicable dans les séries où, parce qu’il y a des termes égaux à zéro ou négatifs , certaines moyennes ne peuvent pas être calculées. C’est également le cas dans les séries homogènes ou lorsqu’il existe de grandes variations entre les termes qui les composent.
- La moyenne arithmétique est également utilisée dans le cas de variations proportionnelles .
Comment calculer la moyenne arithmétique ?
La valeur de la moyenne arithmétique est obtenue en additionnant toutes les données dont nous disposons et en divisant le résultat par le nombre total de ces données.
Les moyennes arithmétiques sont divisées en simples et pondérées :
- Simple : celle qui attribue la même importance aux différents termes de la série ou, exprimée en termes techniques, le même poids, la même pondération.
- Pondéré : celui dans lequel chaque terme de la série de valeurs est influencé par un facteur quantitatif qui le modifie totalement ; comme indiqué, ce facteur quantitatif est appelé poids ou pondération.
Le symbole de la moyenne arithmétique est 
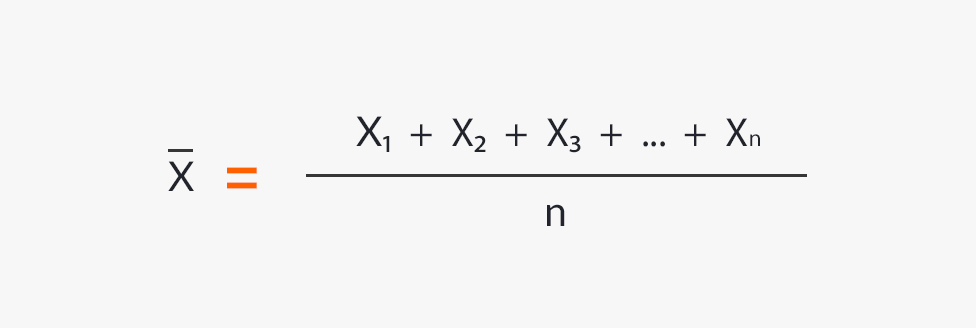
Formule pour calculer la moyenne arithmétique simple.
Compte tenu de ce qui précède, le calcul de la moyenne arithmétique pour les valeurs 4, 6, 8, 10, 16, 28 serait le suivant :
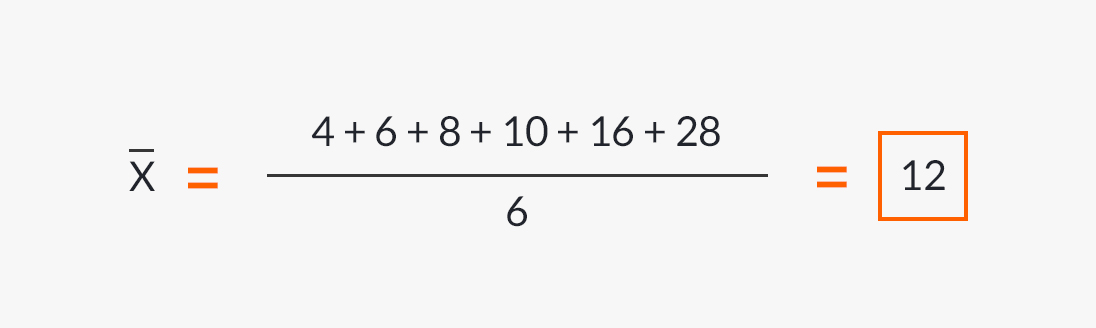
Concernant la moyenne arithmétique pondérée, s’il existe une suite de valeurs X₁, X₂, X₃, …Xn, étant leurs poids respectifs P₁, P₂, P₃, … Pn, la moyenne arithmétique pondérée sera donnée par la formule suivante :
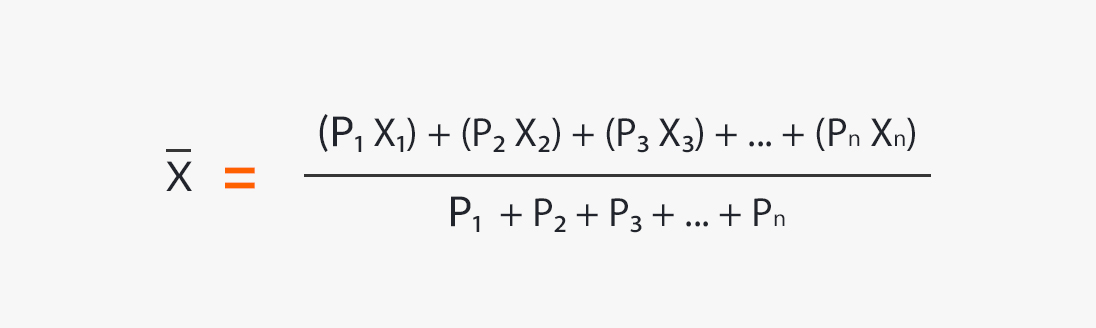
Formule pour calculer la moyenne arithmétique pondérée.
Sur la base de ce qui précède et selon les données suivantes, si différentes unités d’un certain article ont été vendues à des prix différents, comme indiqué ci-dessous…
- 16 unités à US$ 8.
- 20 unités à US$ 5.
- 18 unités à 7 $.
…le calcul du prix moyen pondéré de l’article vendu serait :
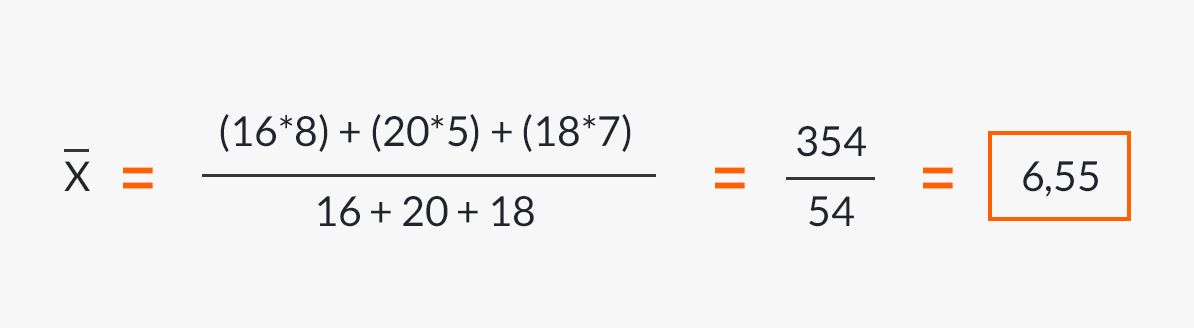
Exemples de moyenne arithmétique
Moyenne arithmétique simple
Voici les âges des 22 joueurs de l’équipe de football brésilienne, qui ont participé au Championnat du monde de football au Mexique en 1970 :
| Joueur | Âge |
|---|---|
| Félix | 32 |
| ado | 25 |
| lis | vingt |
| Britannique | 30 |
| Place Wilson | 27 |
| Charles-Albert | 25 |
| Marc Antoine | 19 |
| Baldochi | 24 |
| Fontaine | 29 |
| Everald | 25 |
| Joël Camargo | 23 |
| Ze Maria | vingt-et-un |
| Clodoaldo | vingt |
| Gerson | 29 |
| pain grillé | 23 |
| Rivelino | 24 |
| Paul César | vingt-et-un |
| Jairzinho | 25 |
| Pelé | 29 |
| robert | 25 |
| Éd | vingt |
| Darius | 24 |
La somme totale des âges est de 540. Pour déterminer l’âge de chacun des membres de l’équipe championne, les années que les joueurs avaient au moment de l’organisation de la Coupe du monde Mexico 70 ont été prises.
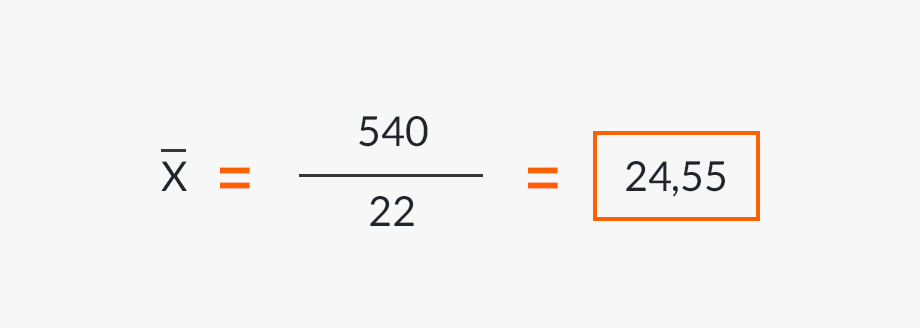
Avec une moyenne d’âge de 24-55 ans, l’équipe brésilienne qui a ébloui les fans de football lors de la Coupe du monde 1970 au Mexique a été, jusqu’à présent, la plus jeune équipe de l’histoire à atteindre cette couronne.
Moyenne arithmétique pondérée
Dans l’entreprise exemple, CA, la masse salariale de 100 travailleurs a la répartition salariale suivante :
| nombre de travailleurs | Salaire mensuel en US$ |
|---|---|
| 40 | 800 |
| 25 | 1 000 |
| vingt | 1 250 |
| quinze | 1 500 |
Les informations ci-dessus seraient organisées comme suit :
| X | Les salaires | 800 | 1 000 | 1 250 | 1 500 | |
| P | Pesée | 40 | 25 | vingt | quinze |
Et afin de déterminer la moyenne arithmétique pondérée, les informations seraient complétées comme suit :
| X | 800 | 1 000 | 1 250 | 1 500 | Total |
| P | 40 | 25 | vingt | quinze | |
| X*P | 32 000 | 25 000 | 25 000 | 22 500 | 104 500 |
D’après cela, le résultat de la moyenne arithmétique pondérée serait :
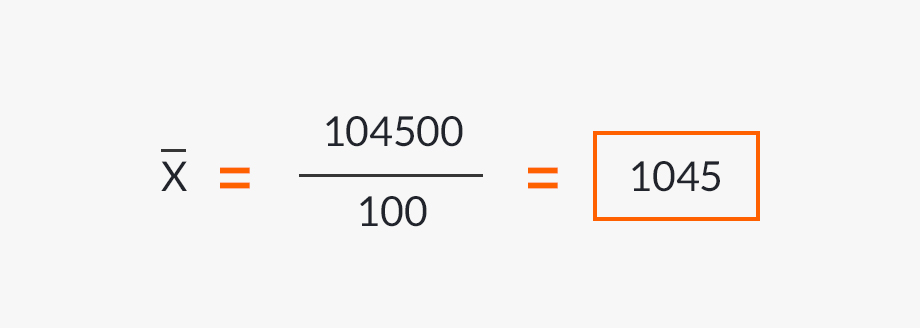
| Bibliographie: |
|---|
|