Type de fréquence statistique utilisé pour déterminer la proportion du nombre de fois qu’une valeur spécifique se produit dans un ensemble total de valeurs.
Qu’est-ce que la fréquence relative ?
La fréquence relative est un type de fréquence statistique utilisé dans la recherche pour déterminer le nombre de fois qu’une valeur spécifique se produit dans un ensemble total de valeurs.
La somme de toutes les fréquences relatives d’un ensemble de valeurs doit toujours être égale à 1, lorsqu’elle est exprimée en décimales, ou égale à 100 % lorsqu’elle est exprimée en pourcentages.
À son tour, la fréquence relative peut être exprimée sous forme de fraction (4/20), de nombre décimal (0,20) ou de pourcentage (20%).
Pour calculer la fréquence relative, la formule suivante est utilisée :
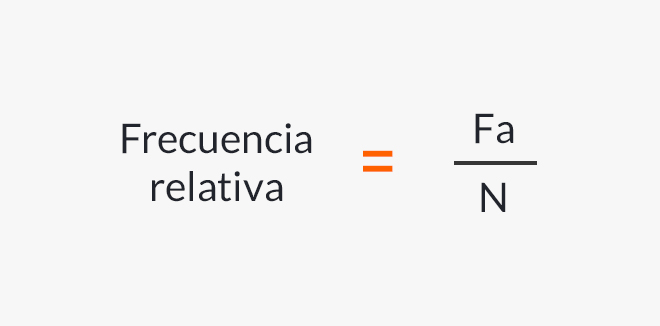
Formule pour calculer la fréquence relative.
Où:
- Fa = fréquence absolue .
- N = Nombre total de valeurs ou d’événements.
Fréquence relative et fréquence absolue
Les concepts de fréquence relative et de fréquence absolue sont des concepts statistiques apparemment similaires, bien qu’ils déterminent en fait des variables différentes.
Certaines distinctions que nous pouvons trouver entre les deux concepts sont les suivantes:
- La fréquence absolue correspond au nombre de fois qu’une valeur est répétée ou, en d’autres termes, au nombre d’événements que présente une certaine caractéristique. D’autre part, la fréquence relative détermine combien de fois la fréquence absolue est répétée dans un ensemble total de données ; de cette manière, c’est la proportion d’événements qui présentent cette caractéristique spécifique calculée en fréquence absolue.
- Pour calculer la fréquence relative , il est nécessaire de disposer au préalable de la valeur calculée de la fréquence absolue, alors que la fréquence absolue peut être calculée indépendamment, sans tenir compte de la fréquence relative.
- La somme des fréquences relatives correspond à 1, si elle est exprimée en décimales, ou à 100 % si elle est exprimée en pourcentages ; tandis que la somme des fréquences absolues correspond au nombre total de données.
Exemples de fréquence relative
Exemple 1
Un consultant décide de mener une enquête sur le nombre d’enfants que les employés d’un bureau ont. Après avoir posé cette question à 20 employés, les réponses sont les suivantes : 0, 2, 2, 0, 3, 1, 1, 2, 3, 1, 0, 2, 3, 4, 3, 4, 2, 0 , 1, 2.
Calculons la fréquence relative :
| Nombre d’enfants | Fréquence absolue | Fréquence relative en décimales | Fréquence relative en pourcentage |
| 0 | 4 | 0,2 | vingt% |
| 1 | 4 | 0,2 | vingt% |
| deux | 6 | 0,3 | 30% |
| 3 | 4 | 0,2 | vingt% |
| 4 | deux | 0,1 | dix% |
| Somme ∑ | vingt | 1 | 100% |
Exemple 2
Supposons que le chercheur décide maintenant d’évaluer la taille des employés de l’organisation, il interroge à nouveau 20 d’entre eux et obtient les résultats suivants : 1,79 ; 1,90 ; 1,82 ; 1,73 ; 1,66 ; 1,77 ; 1,88 ; 1,71 ; 1,72 ; 1,92 ; 1,84 ; 1,87 ; 1,68 ; 1,78 ; 1,96 ; 1,72 ; 1,76 ; 1,90 ; 1.72 et 1.67.
| Hauteur | Fréquence absolue | Fréquence relative en décimales | Fréquence relative en pourcentage |
| [1.60 – 1.70) | 3 | 0,15 | quinze% |
| [1.70 – 1.80) | 9 | 0,45 | Quatre cinq% |
| [1.80 – 1.90) | 4 | 0,2 | vingt% |
| [1.90 – 2.00) | 4 | 0,2 | vingt% |
| Somme ∑ | vingt | 1 | 100% |
| Bibliographie: |
|---|
|