Racine carrée dérivée d’un écart type.
Qu’est-ce que la variance ?
La racine carrée qui découle d’un écart -type est appelée variance , ce qui permet aux industries manufacturières de travailler avec précision dans leur production et de réduire leur taux d’erreur.
La variance extrait les données dispersées de la moyenne et, après l’avoir mesurée, donne une valeur aux variations et aux écarts. De plus, il permet de compter et d’éviter d’éventuelles erreurs.
A quoi sert l’écart ?
En proposant l’utilisation de la variance, Ronald Fisher a mentionné qu’elle servirait à connaître et à considérer la valeur moyenne d’une variable. À tel point que la variance a été créée pour déterminer si les différences qui existent entre les moyennes de l’échantillon exposent les différences qui existent entre les valeurs moyennes.
De cette manière, la valeur est identifiée au moyen d’une racine carrée qui permet de connaître la difficulté de la marge d’erreur et, de même, de réaliser un plan spécifique et réussi.
La variance est utilisée par les entreprises et les industries comme méthode de prévention et de visualisation vers l’avenir.
Formule pour calculer la variance
La formule la plus utilisée pour calculer la variance est la suivante :
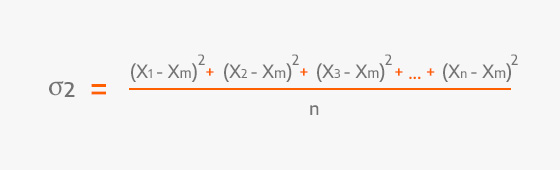
Formule pour calculer la variance.
La variance est représentée par » σ² », une lettre grecque sigma au carré.
La valeur de Xm est obtenue par la moyenne arithmétique ou la moyenne des valeurs à analyser, tandis que Xn est obtenue par la valeur à analyser .
exemple d’écart
Pour mieux comprendre ce concept, nous proposons l’exemple d’ une entreprise qui souhaite calculer la variance des tonnes de nourriture qu’elle a vendues au cours des 6 derniers mois :
| Mois | quantité vendue |
|---|---|
| Janvier | 18 |
| Février | vingt |
| Mars | vingt |
| Avril | 22 |
| Peut | vingt |
| Juin | vingt |
La première étape du calcul de la variance consiste à calculer la moyenne arithmétique (la moyenne ). Ceci est obtenu en tenant compte du fait que le nombre de valeurs à analyser est de 6 (les 6 derniers mois) :
(18 + 20 + 20 + 22 + 20 + 20) / 6 = 20
Une fois la moyenne arithmétique obtenue, dans ce cas 20, nous procédons au calcul de la variance, en utilisant la formule susmentionnée :
σ² = [(18-20) 2 + (20-20) 2 + (20-20) 2 + (22-20) 2 + (20-20) 2 + (20-20) 2 ] / 6 = 1, 33
De cette manière, nous obtenons une variance (σ²) de 1,33 .